Kerala School of Mathematics frequently conducts regular colloquiums and seminars by eminent and established mathematicians and upcoming researchers. The details of the various colloquiums and seminars at KSoM can be found below
KSoM Colloquium Talk
Title: Arcs in algebraic varieties
Speaker: Prof. Aravind Nair
Affiliation: Tata Institute of Fundamental Research (TIFR), Mumbai
Venue: Seminar Hall, KSoM
Date and Time: May 8, 2025, 3:30 to 4:30 PM
Abstract: Various spaces of arcs in algebraic varieties have recently become of interest in several contexts of both algebraic geometry and representation theory. I will discuss some of these results.
KSoM Colloquium Talk
Title: A tale of two semigroups
Speaker: Sundaram Thangavelu
Affiliation: Indian Institute of Science, Bangalore
Venue: Seminar Hall, KSoM
Date and Time: April 30, 2025, from 4 to 5 PM
Abstract: On $ L^p(\R^{2n}) $, we have two semigroups of operators generated by Hermite and special Hermite operators. A curious relation between these two semigroups was discovered recently. We will talk about this and some applications if time permits.
KSoM Seminar Talk
Title: Braid group and its representations
Speaker: Athira E V , Research Scholar, KSoM
Venue: Seminar Hall, KSoM
Date and Time: April 30, 2025 [Wednesday] at 2:00 PM
Abstract: Inspired by Curtis T. McMullen’s work ”Braid groups and Hodge theory,” this talk journeys into the unitary representations of the braid group. We will first establish the necessary foundations by reviewing braid groups, mapping class groups, Hodge de-composition, and irreducible representations. Along the way, we will draw upon concept from covering space theory, differential forms, Dehn twists, Hodge theory, the theory of Riemann surfaces, and the cohomology of exact sequences, as well as basic representation theory. Our ultimate goal is to achieve a comprehensive understanding of unitary braid group representations and description of all finite-sheeted cyclic branched covers of the Riemann sphere.
David Hilbert Colloquium
Title: Hilbert’s Finiteness Theorem for Invariants
Speaker: Vasudevan Srinivas
Affiliation: University at Buffalo
Venue: Seminar Hall, KSoM
Date and Time: January 3, 2025 at 5:00 PM
Abstract: This talk will give an introduction to Hilbert’s work on invariant theory, which includes the novel use of the Hilbert basis theorem and the Hilbert syzygy theorem. This work led to the development of modern invariant theory, and initiated the field of commutative algebra. An accessible source is a translated version of his lecture notes: Theory of Algebraic Invariants, David Hilbert, translated by Reinhard C. Laubenbacher, Cambridge Mathematical Library, Cambridge University Press (1993).

Research Talk
Speaker:Aparna Pradeep V K
Affiliation: KSoM
Venue: Seminar Hall, KSoM
Date and Time: December 30, 2024 at 3:30 PM.
Title: On a Study of Unitary Groups and ESD Transvection Groups.
Abstract: In 1976, L.N. Vaserstein used a construction analogous to Gram–Schmidt orthogonalisation, for obtaining a set of symplectic matrices from a set of elementary matrices. We made a similar construction for Petrov’s odd unitary group. In this talk, I will explain this construction and show that the elementary matrices in the odd unitary analogue of the Gram-Schmidt process form a set of generators for the elementary group. Also, we will prove the equality of the Eichler-Siegel-Dickson transvection group and the DSER elementary orthogonal group introduced by A. Roy in 1968. Moreover, I will discuss a problem on commutator calculus for classical unitary groups, which we are trying to generalise to the Bak’s unitary group.
Research Talk
Speaker: Shivani Goel
Venue: Seminar Hall, KSoM (Online)
Date and Time: November 27, 2024 at 3:30 PM
Title: Matrices related to graphs.
Abstract: Given a graph (directed or undirected), one can associate different matrices. Among these, adjacency matrix, distance matrix and resistance distance matrix are some of the most interesting topics in recent times. In this talk, we will discuss some recent results and future scope of work on distance, resistance and some newly defined matrices on graphs.
From a given finite group, several type of graphs can be generated. Some of the graphs that arises from the combinatorial properties of groups are power graphs and enhanced power graphs. We will conclude by exploring the spectrum of adjacency and distance matrices related to such graphs.
Research Talk
Speaker:Sanjoy Chatterjee
Affiliation: Indian Statistical Institute, Kolkata
Venue: Seminar Hall, KSoM (Online)
Date and Time: November 22, 2024 at 2:00 PM
Title:Approximation of biholomorphisms on certain domains in complex manifolds.
Abstract:In this
talk, we will discuss the domains in
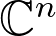
that are invariant under the positive time flows of some globally defined, complete holomorphic vector field with a globally attracting fixed point inside the domain. We will show that such a domain

is always Runge. Next, with an additional assumption on the rate of convergence of the flow, we show that any bi- holomorphism
)
, with
)
is Runge, can be approximated by elements of automorphisms of
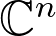
uniformly on compacts. We will provide an application of our approximation result in the context of Loewner PDE. Finally, we will show that the analogous approximation result also holds on certain complex manifolds.
Research Talk
Speaker:Subhankar Sau
Affiliation: Indian Statistical Institute, Kolkata
Venue: Seminar Hall, KSoM (Online)
Date and Time: November 20, 2024 at 3:30 PM
Title: Resolution of singularity of quasitoric orbifolds
Abstract: Resolution of singularity is a classical problem in Geometry and Topology. In this talk, we discuss the techniques of resolution of singularity. We recall the constructive definition of quasitoric orbifolds. We define blowups, blowdowns and k-wedge constructions of quasitoric orbifolds. Eventually, we prove that there exists at least one resolution of singularity of any quasitoric orbifold.
Research Talk
Speaker: Srijonee Shabnam Chaudhury
Venue: Seminar Hall, KSoM (Online)
Date and Time: November 15, 2024 at 3:30 PM
Title: Universal Quadratic Forms over Number Fields and related topics
Abstract: In this talk we introduce the basic notion of quadratic forms over number fields. After that we discuss, for any given positive integer m, how to construct certain totally positive algebraic integers α of a real bi-quadratic field as well as complex number field K. Using this we obtain some necessary conditions for which mα can not be represented as sum of integral squares. We also show a relation between the class number and universal ℤ-forms over totally real number fields K of degree less than 7. Finally, in the last part we exhibit a best-possible lower bound of Trace-2 measure of a family of symmetric and symmetrizable positive-definite integer matrices. Moreover, we show that the famous result of Smyth on density of absolute trace measure of totally positive integers is also true for the set of symmetric integer connected positive definite matrices.
Research Talk
Speaker: Arun Kumar Bhardwaj
Venue: Seminar Hall, KSoM (Online)
Date and Time: November 13, 2024 at 3:30 PM
Title: The Space of Multipliers between Model Spaces: Complete or Incomplete?
Abstract: Let  be an inner function in the unit disk, that is, a bounded analytic function in the unit disk with unimodular nontangential limit on the boundary. To each inner function, we can obtain a Hilbert space, namely, the model space
be an inner function in the unit disk, that is, a bounded analytic function in the unit disk with unimodular nontangential limit on the boundary. To each inner function, we can obtain a Hilbert space, namely, the model space  on the unit disk, which is nothing but the backward shift invariant subspace of the Hardy space
on the unit disk, which is nothing but the backward shift invariant subspace of the Hardy space  . These spaces play a crucial role in Complex analysis, Harmonic analysis, Operator theory, etc. For inner functions
. These spaces play a crucial role in Complex analysis, Harmonic analysis, Operator theory, etc. For inner functions  and
and  , an analytic function
, an analytic function  on the unit disk is said to be a multiplier from the spaces
on the unit disk is said to be a multiplier from the spaces  into
into  if
if  . The collection of multipliers from the spaces
. The collection of multipliers from the spaces  into
into  is denoted by
is denoted by ) . In 2018, E. Fricain, A. Hartmann, and W. Ross first studied the multipliers between two different model spaces of
. In 2018, E. Fricain, A. Hartmann, and W. Ross first studied the multipliers between two different model spaces of  . In this talk, we aim to investigate the completeness of these spaces of multipliers. Suppose
. In this talk, we aim to investigate the completeness of these spaces of multipliers. Suppose  and
and  are inner functions such that
are inner functions such that  divides
divides  . In this case, we completely characterize the completeness of the space of multipliers
. In this case, we completely characterize the completeness of the space of multipliers ) . It is known from previous studies that the space
. It is known from previous studies that the space ) is closely related to certain Carleson measures for the model space
is closely related to certain Carleson measures for the model space  . We have completely characterized the Carleson measures for
. We have completely characterized the Carleson measures for  generated by functions of
generated by functions of  , where
, where  is a non-negative integer. As a consequence, we can describe the space
is a non-negative integer. As a consequence, we can describe the space ) completely.
completely.
Colloquium by Prof. Joseph Mathew
Title: Van der Waerden’s Theorem
Speaker: Joseph Mathew
Affiliation:ISI Kolkata (Former)
Venue: Seminar Hall, KSoM
Date and Time: November 12, 2024 [Tuesday] at 04:00 PM
Abstract: If the set of natural numbers N is a union of the subsets C(1), C(2), …, C(r), of N, then there is a C(i) that will contain arbitrary long arithmetic progressions. I will sketch a topological dynamics proof of the above theorem, and will talk about generalisations of it.
Augustin Cauchy Colloquium
Title: Imbedding of critical Fractional Sobolev Spaces
Speaker: Adi Adimurthi
Affiliation: TIFR CAM
Venue: Seminar Hall, KSoM
Date and Time: August 2, 2024 at 3:30 PM
Abstract: It is shown by Dyda that for  or
or  , fractional Sobolev spaces are embedded in Weighted Lebesgue spaces with weight
, fractional Sobolev spaces are embedded in Weighted Lebesgue spaces with weight %5E%7B-sp%7D) . He also showed that it is optimal and it will not be true for
. He also showed that it is optimal and it will not be true for  , the critical case. In this talk I will address this problem and show what is the correct weight to be taken in the imbedding. This is a joint work with Prosenjit Roy, Purbita Jana and Prosenjit Roy, Vivek Sahu.
, the critical case. In this talk I will address this problem and show what is the correct weight to be taken in the imbedding. This is a joint work with Prosenjit Roy, Purbita Jana and Prosenjit Roy, Vivek Sahu.

Alan Turing Colloquium.
Title: Do stochastic parrots pass the Turing test?
Speaker: Madhavan Mukund
Affiliation: Chennai Mathematical Institute
Venue: Seminar Hall, KSoM
Date and Time: June 14, 2024 at 3:30 PM
Abstract: Alan Turing not only laid the foundations of modern computing science, he was also one of the pioneers of artificial intelligence. He formulated the imitation game, more commonly called the Turing test, to establish whether a computing system exhibits intelligence. Large language models such as ChatGPT have been all over the news recently. Some people claim these systems exhibit evidence of “emergent intelligence”. We describe how such systems are built and address some of the philosophical questions surrounding their capabilities.
KSoM Colloquium talk
Title: Finite and Infinite dimensional Lie algebras
Speaker: Punita Batra
Affiliation:Harish-Chandra Research Institute, Prayagraj
Venue: Seminar Hall, KSoM
Date and Time: June 11, 2024 [Tuesday] at 03:30 PM
Abstract: I will discuss about finite dimensional simple Lie algebras with examples, semisimple Lie algebras, define some basic terms and give a realisation of affine Kac-Moody Lie algebras and discuss toroidal Lie algebras.
KSoM Colloquium talk
Title: On the trace of powers of Algebraic integers
Speaker: R. Thangadurai
Affiliation:Harish-Chandra Research Institute, Prayagraj
Venue: Seminar Hall, KSoM
Date and Time: June 10, 2024 [Monday] at 11:00 AM
Abstract: Let

be a non-zero algebraic integer. In this lecture, we prove an interesting characterisation for

to be a root of unity, which is an extension of a classical theorem of Kronecker. Indeed, we prove that {\it if a non-zero algebraic integer

is a root of unity if and only if the sequence
/%5Cmathbb%7BQ%7D%7D(%5Calpha%5En)%5Cright)%5F%7Bn%5Cgeq%091%7D)
is bounded. Moreover, if the sequence
/%5Cmathbb%7BQ%7D%7D(%5Calpha%5En)%5Cright)%5F%7Bn%5Cgeq%091%7D)
is bounded, then it is periodic.} Thus, if a non-zero algebraic integer

is not a root of unity, it is clear that the sequence
/%5Cmathbb%7BQ%7D%7D(%5Calpha%5En)%5Cright)%5F%7Bn%5Cgeq%091%7D)
is unbounded and hence we study the growth in the next result. Also, we introduce a problem of Polya and its extensions.
KSoM Research Talk
Speaker: Viswanathan S
Affiliation: ICTS Bangalore
Venue: Seminar Hall, KSoM
Date and Time: June 03, 2024 at 3:30 PM
Title: Introduction to Teichmüller Spaces
Abstract: Teichmüller spaces have proven to be effective tools to study moduli spaces of Riemann surfaces. It has also found natural applications in dynamics, geometry, and topology. The purpose of this talk would be to introduce these spaces from several perspectives to hammer home the point that the theory at heart brings together algebra, geometry, and analysis.
The Henri Poincare Colloquium.
Title: Bargmann and Fock meet Hardy: An uncertainty principle for operators.
Speaker: S. Thangavelu
Affiliation: Indian Institute of Science, Bangalore
Venue: Seminar Hall, KSoM
Date and Time: April 5, 2024 at 3:30 PM
Abstract: Heisenberg uncertainty principle in Quantum Mechanics states that the position and momentum of a moving particle cannot both be measured simultaneously. Viewed as an interesting property of the Fourier transform, this principle has several different manifestations in the realm of Fourier Analysis, including a theorem of Hardy studied extensively by the Indian harmonic analysts. Quite unexpectedly, this principle of Hardy shows its ugly head (or charming face) in connection with the boundedness of certain convolution type operators on the Fock space. The key player is Bargmann who connects Schrodinger with Fock and as expected, Hermite has his own role to play. We plan to describe this story with as little details as possible.

One day session on “Engaging Liminal Spaces in Mathematics with Social Sciences”
Liminal space refers to a place the person is in during a transition phase. Exactly where, aspiring mathematicians are till they become mathematicians (and thereafter!!!). We work on various problems: real, imaginary and imagined (infinite) juggled around with logic in our heads to come up with propositions and theorems-approximating, affirming and at times even vanishing. Well managed! Then there are other non-mathematical problems. Again, real, imaginary and imagined, but related to – non, in, extra, and ultra-variants of – human. With these problems in our head, we head nowhere. Ill managed!
Mind matters, and minds at large matter too!
Social sciences concern human worlds and society; how individuals and groups interact and what drives human behavior. Let us gather on 13 March, 2024, for an engaging one day session, by (in order) a real, imaginative and hyperbolic social scientist.
Dr. Neetulal (Dept. of Psychology, University of Calicut)
Dr. Kiran S (Dept. of Psychology, University of Calicut)
Prof. A. F. Mathew (Humanities & Liberal Arts in Management, IIMK)
to help us make the ill managed, well managed and to connect better with this not too familiar entity called ‘society’ when we are in our liminal spaces.
Co-ordinators
Ramshida A. P. (Dept. of Psychology, University of Calicut)
Pranav Haridas (KSoM)
Radhika M. M. (KSoM)

The Alexander Grothendieck Colloquium
Title: Integrals over the
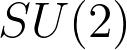)
character variety and lattice gauge theory.
Speaker: T R Ramadas
Affiliation: Chennai Mathematical Institute
Venue: Seminar Hall, KSoM
Date and Time: March 1, 2024 at 3:30 PM
Abstract: Given a genus-
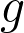
Riemann surface
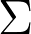
, the moduli space of rank two vector bundles with trivial determinant is, by the Narasimhan-Seshadri Theorem, in bijection with the space of (equivalence classes of) representations in
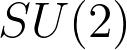)
of the fundamental group of the surface .
In the latter avatar, this space has a symplectic structure and a corresponding finite measure, the Liouville measure. Normalising to total mass one gives a probability measure. There is a natural class of real-valued functions parameterised by isotopy classes of loops on the surface. These are called Wilson loop functions by physicists and Goldman functions by mathematicians. I present a simple scheme to compute joint distributions of these functions for families of loops. This is possible because of the miracle of symplectic geometry called the Duistermaat-Heckman formalism (whose applicability in this context is due to L. Jeffrey and J. Weitsman), and a continuous analogue of the Verlinde algebra.
The large
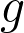
asymptotics can be easily read off.
This leads to a highly speculative approach to rigorous analysis of (lattice) gauge theories, as a preliminary step to quantum-field-theoretic constructions.

David Hilbert Colloquium
Title: Free groups
Speaker: Parameswaran Sankaran
Affiliation: Chennai Mathematical Institute
Venue: Seminar Hall, KSoM
Date and Time: January 19, 2024 at 3:30 PM
Abstract: Free groups are free objects in the category of groups and as such can be defined in terms of a certain universal property. They arise in geometry, topology, besides group theory itself. After discussing some of their basic properties, we will show that many familiar groups contain (non-abelian) free groups. The talk will be accessible to graduate students and non-specialists.
Title: Multiplication operators on Hardy space
Speaker: Aneesh M
Affiliation: Indian Institute of Technology, Bhubaneswar
Venue: Seminar Hall, KSoM
Date and Time: December 22, 2023 at 3:00 PM
Abstract: This is a short introduction to the subject Dynamics of Linear Operators which is at the
cross-road of functional analysis, complex analysis, and dynamical systems. We review a few well known dynamical properties (such as the hypercyclicity and chaos) of multiplication operators on the Hardy-Hilbert space
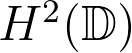)
which consists of all analytic functions on the unit disc

, whose Taylor coefficients belong to

. A multiplication operator is given by
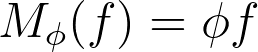%09=%09%5Cphi%09f)
on
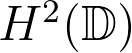)
, where
is necessarily a bounded analytic function. When
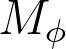
is a bounded operator, the closure of the range
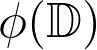)
is the spectrum of
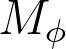
, and the range itself is the point spectrum of the adjoint
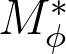
, and the eigenvectors are nothing but the reproducing kernels at each point of

. These facts along with certain classical results about chaotic operators yield the following: the adjoint
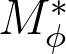
is chaotic on
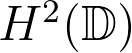)
if and only if
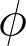
is non-constant and
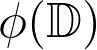)
intersects the unit circle
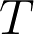
. This result is not true for some other Hilbert spaces of analytic functions, such as the Dirichlet space. We will also see a few open problems that are fairly simple to state, yet unsolved so far.
National Mathematics Day Colloquium
Title: The Problem of Structural Stability
Speaker: Shiva Shankar
Venue: Seminar Hall, KSoM
Date and Time: December 22, 2023 at 12 PM
Abstract: The development of a scientific discipline usually follows the pattern of experimental observations, construction of a theoretical model, and an interpretation of its predictions. In order to be useful, the model’s predictions must not be sensitive to the values of the various parameters that appear in its description. This is the criterion of `Stability’. I will explain this in the context of ‘structural stability’ of dynamical systems, first enunciated by Andronov and Pontriagin, and founded on ideas going back to Newton’s treatment of the 3-body problem.

John Von Neumann Colloquium
Title : What is involved in Quantum Mechanics?
Speaker: Krishna Maddaly
Affiliation: Ashoka University
Venue: Seminar Hall, KSoM
Date and Time: December 08, 2023 at 3:30 PM
Abstract: Quantum Mechanics emerged as a need to explain many natural phenomena that occur at very small scales and took a while to formulate precisely. In this journey John von Neumann played a crucial role to give a firm Mathematical foundation to the theory. In this talk I will explain the theory and the role of von Neumann.
Title: കേരളത്തിന്റെ പ്രാദേശിക ഗണിത ശാസ്ത്രവ്യവഹാരങ്ങൾ :താളിയോല ഗ്രന്ഥങ്ങളിലൂടെ (Regional Mathematical Discourses of Kerala: Through Palm Leaf Texts.)
Speaker: Dr. Manju M. P.
Affiliation: Department of Malayalam and Kerala Studies, University of Calicut
Venue: Seminar Hall, KSoM
Date and Time: November 01, 2023 at 11:30 AM
Abstract: ഈ പ്രബന്ധത്തിൽ കേരളത്തിന്റെ പ്രാദേശിക ഗണിതവ്യവഹാരങ്ങളെ കുറിച്ചാണ് പറയാൻ ശ്രമിക്കുന്നത്. അതിനു വേണ്ടി കേരളത്തിലെ, താളിയോല ഗ്രന്ഥശേഖരങ്ങളിലെ (പ്രധാനമായും കാലിക്കറ്റ് സർവ്വകലാശാല തുഞ്ചൻ മാനുസ്ക്രിപ്റ്റ് റപോസിറ്ററിയിലെ )ഗണിത സംബന്ധിയായ ഗ്രന്ഥങ്ങളെ പഠനവിഷയമാക്കുന്നു. ഗ്രന്ഥശേഖരത്തിലെ പ്രധാന ഗണിതഗ്രന്ഥങ്ങളെ പരിചയ പെടുത്തുക എന്നതാണ് പ്രബന്ധത്തിന്റെ പ്രധാന ലക്ഷ്യം. അതിനോടൊപ്പം ഇതിൽ നിന്ന് ഒരു താളിയോലഗ്രന്ഥത്തെ പ്രധാന പഠനവസ്തുവായി എടുത്ത് പഠിക്കുകയും ചെയ്യുന്നു. ഇത് വഴി കേരളത്തിന്റെ ജ്ഞാനസമ്പത്ത് , അതിന്റെ കൈവഴികൾ എന്തെല്ലാം തുടങ്ങിയ കാര്യങ്ങളും പറയുന്നു പ്രബന്ധത്തിനോട് അനുബന്ധമായി ഹസ്തലിഖിത വിജ്ഞാനീയത്തിലെ പ്രാചീന എഴുത്തുപാരമ്പര്യത്തെയും പരിചയപ്പെടുത്തുന്നു.
Title: Prime numbers
Speaker: Kalyan Chakraborty
Affiliation: Harish-Chandra Research Institute, Prayagraj
Venue: Seminar Hall, KSoM
Date and Time: September 01, 2023 at 3:30 PM
Abstract: Several historical questions regarding prime numbers are still unsolved. These include Goldbach’s conjecture, that every even integer greater than 2 can be expressed as the sum of two primes, and the twin prime conjecture, that there are infinitely many pairs of primes that differ by two. Such questions spurred the development of various branches of number theory, focusing on analytic or algebraic aspects of numbers. Primes are used in several routines in information technology, such as public-key cryptography, which relies on the difficulty of factoring large numbers into their prime factors.
Title: p-numerical semigroups and their fundamental properties
Speaker: Takao Komatsu
Affiliation: Zhejiang Sci-Tech University
Venue: Seminar Hall, KSoM
Date and Time: August 05, 2023 at 3:30 PM
Abstract: Consider the linear Diophantine equation
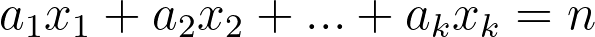
, where
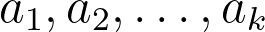
are positive integers and
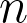
is a non-negative integer. When we want to know the non-negative solutions, the number of solutions is finite if and only if
=1)
. For a given non-negative integer
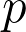
, there exists the largest integer
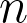
such that the number of solutions is at most
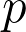
. We call this largest integer the
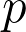
-Frobenius number. When

, the
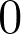
-Frobenius number is the classical Frobenius number, which is the central role of the famous linear Diophantine problem of Frobenius. In this talk, we introduce the basic concept of the
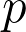
-numerical semigroup and mention the fundamental properties. We describe how the
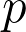
-Frobenius number and related values are obtained.
Title: Group actions in non-commutative geometry.
Speaker: Safdar Quddus
Affiliation: Indian Institute of Science, Bangalore
Venue: Seminar Hall, KSoM
Date and Time: July 31, 2023 at 12:00 PM
Abstract: Historically, it is well known that group action changes the homological, differential, and topological properties of manifolds. The aim of this talk is to discuss the action of finite groups on some non-commutative differential and algebraic spaces. We shall first discuss the (co)homological properties of non-commutative and quantum torus then observe how the quotient spaces resulting from the actions of discrete subgroups of
)
behave, and then shall discuss the flip actions on the non-commutative sphere. We shall see how the tools are developed in non-commutative geometry to understand and tackle the group action in general non-commutative spaces.
Title: Rational points on hyperelliptic curves.
Speaker: Om Prakash
Affiliation: Kerala School of Mathematics
Venue: Seminar Hall, KSoM
Date and Time: July 28, 2023 at 2:30 PM
Abstract: Hyperelliptic curves which can be viewed as generalisation of elliptic curves are a special class of algebraic curves. The theory of elliptic curves is sort of well understood and has a vast literature. However, the theory of hyperelliptic curves has not received as much attention by the research community; and most results concerning hyperelliptic curves which appear in the literature on algebraic geometry are couched in very general terms. In this talk we give an overview of results concerning rational points on hyperelliptic curves and present our recent joint work with Kalyan Chakraborty.
Title: Hyperbolicity of the Curve Graph
Speaker: George Shaji
Affiliation: Department of Mathematics, The University of Utah
Venue: Seminar Hall, KSoM
Date and Time: July 26, 2023 at 11:00 AM
Abstract: We will briefly explore the “Guessing Geodesics Lemma”, and see its immense usefulness by applying it to the curve graph of a surface. Specifically, we shall show that the Curve Graph of a finite type surface (of sufficient complexity) is hyperbolic using “Unicorn Paths” or “Bicorn Paths”. This method provides an extremely beautiful, diversely applicable and significantly simpler alternative to the Masur-Minsky machinery used to prove the same fact much earlier.
Title: M-ideals in the Algebra of bounded analytic functions
Speaker: Sreejith Siju
Affiliation: Kerala School of Mathematics
Venue: Seminar Hall, KSoM
Date and Time: July 25, 2023 at 3:00 PM
Abstract: The distinguished class of subspaces of a Banach space known as M -ideals is a significant tool in the study of the geometry of Banach spaces and approximation theory. The M-ideals in the continuous functions space and the disk algebra are fairly understood. In this talk we will discuss some basic facts regarding M-ideals and some recent results on M-ideals in the algebra of bounded analytic functions. This talk is based on a joint work with Deepak and Jaydeb.
Title: On a class of Lebesgue-Ramanujan-Nagell equations
Speaker: Azizul Hoque
Affiliation: Department of Mathematics, Rangapara College
Venue: Seminar Hall, KSoM
Date and Time: July 21, 2023 at 11:00 AM
Abstract: Finding the solutions of an exponential Diophantine equation is a classical problem and even now it is a very active area of research. One of the most important equations of this type is so-called Lebesgue-Ramanujan-Nagell equation,
=1,%09%5Clambda=1,2,4),)
where

is a fixed positive integer. In this talk, we will discuss some interesting results concerning the integer solutions of certain generalizations of the above equation. This talk is based on some joint works with K. Chakraborty and K. Srinivas.
Title: Selmer group associated to the group of degree zero cycles on abelian varieties
Speaker: Kalyan Banerjee
Affiliation: Vellore Institute of Technology, Chennai
Venue: Seminar Hall, KSoM
Date and Time: July 11, 2023 at 3:00 PM
Abstract: In this talk we will look into a construction of the Selmer group of degree zero cycles on abelian varieties and will prove that it is finite.
Title: Genuinely ramified maps and the Galois group of generic projection
Speaker: Parameswaran A J
Affiliation: TIFR, Mumbai
Venue: Seminar Hall, KSoM
Date and Time: April 13, 2023 at 12:00 PM
Abstract: We show that the Galois closure of a degree d genuinely ramified covering
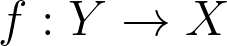
of smooth projective irreducible curves over an algebraically closed field is the symmetric group

if
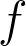
is a Morse map.
Title: Jordan derivations and 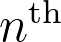 -power property in rings
-power property in rings
Speaker: Shakir Ali
Affiliation: Aligarh Muslim University
Venue: Seminar Hall, KSoM
Date and Time: February 08, 2023 at 12:00 PM
Abstract: Let
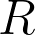
be an associative ring(algebra) with center
)
. Every associative ring
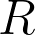
can be turned into a Lie ring(algebra) by introducing a new product
![[x, y] = xy - yx [x, y] = xy - yx](https://ci6.googleusercontent.com/proxy/w3dLcLQLNPTQJs-JvV4ZxRY-ltlVHJMvrz2DQ8eHNUJQCJwafM5-9bVRV8TrYyHI2_YJ4YbDon88RBfj6hgfsAhY-KVRPz4jbgKMYfRZTjoJSAX2HGuupPyt9zihhq8JkVAlvkRpAnRGMXXzTQ4=s0-d-e1-ft#https://s0.wp.com/latex.php?zoom=3&bg=ffffff&fg=000000&s=0&latex=[x,%09y]%09=%09xy%09-%09yx)
, known as the Lie product. So we may regard
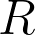
simultaneously as an associative ring(algebra) and as a Lie ring(algebra). An additive mapping
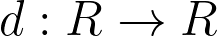
is said to be a derivation on
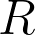
if
%09=%09d(x)y%09%2B%09xd(y))
holds for all
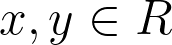
. An additive mapping

is said to be a Jordan derivation if
%09=%09d(x)x%2Bxd(x))
holds for all
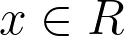
. A function
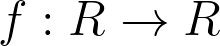
is called a centralizing on
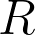
if
![[f(x), x)] \in Z(R) [f(x), x)] \in Z(R)](https://ci3.googleusercontent.com/proxy/hcWGwnPabyudf2EgRc9JBD53ICI5EsFTG-gorv10I4fXbcViH7jDlo3hMoboHdtGpDb3m2zyOSHJKq0-pX2oE2CiBkT1zDRhyYo2sQ9WaY0tHejK45JWfTvgEBHRhgMpo9htWPfqky6cqD2q2Ai4=s0-d-e1-ft#https://s0.wp.com/latex.php?zoom=3&bg=ffffff&fg=000000&s=0&latex=[f(x),%09x)]%09%5Cin%09Z(R))
holds for all
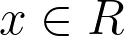
. In the special case where
![[f(x), x)] = 0 [f(x), x)] = 0](https://ci6.googleusercontent.com/proxy/scCk0vrVrZbO1NhWXgOhnLbCW8GieEPHOhzfSwjR7mqCbF1AcSvqPhAuRALBRiP-IPOeb09iO6jHcz66U_0M9ec-ry3nXukvfl-KLeZ8n-QpsZF31xo94_Dqru7dp5b3akFfyclLao4=s0-d-e1-ft#https://s0.wp.com/latex.php?zoom=3&bg=ffffff&fg=000000&s=0&latex=[f(x),%09x)]%09=%090)
for all
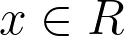
,
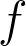
is said to be commuting on
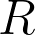
. The study of such mappings was initiated by E.C. Posner [ Proc. Amer. Math. Soc. 8(1957), 1093-1100]. In 1957, he proved that if a prime ring
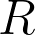
has a nonzero commuting derivation on
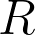
, then
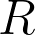
is commutative. An analogous result for centralizing automorphisms on prime rings was obtained by J.H. Mayne [Canad. J. Math. 19 (1976), 113-115].
In this talk, we will discuss the recent progress made on the topic and related areas. Moreover, some examples and counterexamples will be discussed for questions raised naturally.
Title: Inversion formulas for the 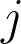 -function around elliptic points.
-function around elliptic points.
Speaker: Badri Vishal Pandey
Affiliation: Universität zu Köln, Germany
Venue: Seminar Hall, KSoM
Date and Time: February 02, 2023 at 12:00 PM
Abstract: Recently, Hong, Mertens, Ono, and Zhang proved a conjecture of Căldăraru, He, and Huang that expresses the Taylor series of the modular
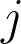
-function around the elliptic points
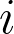
and
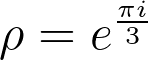
as rational functions arising from the signature
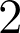
and

cases of Ramanujan’s theory of elliptic functions to alternative bases. We extend these results and give inversion formulas for the
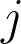
-function around
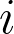
and
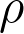
arising from Gauss’ hypergeometric functions and Ramanujan’s theory in signatures
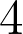
and
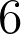
.
Title: Non-archimedean dynamics in dimension one
Speaker: Niladri Patra
Affiliation: Tata Institute of Fundamental Research, Mumbai
Date and Time: December 09, 2022 at 03:30 PM
Venue: Seminar Hall
Abstract: In the beginning of the twentieth century, complex analysis gave rise to complex dynamics, which is the study of self-iterations of rational maps defined over complex numbers. Often the study of complex dynamical objects boil down to questions that are of arithmetic nature. This generally motivates the study of arithmetic dynamics. Arithmetic dynamics is roughly divided into two parts, dynamics over global fields and dynamics over local fields. Dynamics over local fields, which is also called non-archimedean dynamics or p-adic dynamics in the literature, has another motivation coming from p-adic analysis. The motivation is to build a theory parallel to complex dynamics with field of complex numbers replaced with
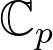
. The theory that follows is called classical p-adic dynamics. One finds certain anomalies between the theories of complex dynamics and classical p-adic dynamics. These anomalies mostly arise from the fact that unlike
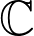
, the topological field
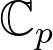
is totally disconnected and not locally compact. To rectify these issues, one replaces
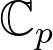
(or,
)
) with the Berkovich projective line, which is compact, Hausdorff, path connected space and in which
)
embeds. In this talk, we will introduce discrete, complex, classical p-adic dynamics, dynamics on the Berkovich projective line and mention some of the parallels between complex dynamics and dynamics on the Berkovich projective line.
Tittle : RESULTS AND MODELS. AN ILLUSTRATION THROUGH SUMS OF CUBES
Speaker : Jean-Marc Deshouillers
Affiliation : University of Bordeaux, France.
Date and Time : 24-09-2022 at 03;30 PM
Venue : Seminar hall, Kerala School of Mathematics
Abstract :
RESULTS AND MODELS. AN ILLUSTRATION THROUGH SUMS OF CUBES
Number theory has the knack for phrasing easily understandable statements which are hard to prove.
An archetype is Goldbach’s problem (1742), which is still unsolved : every even integer larger than 4 is a sum of two primes.
The root of the talk is Waring’s problem (1770), which states – for cubes – that every integer is a sum of at most 9 cubes. It has been proved in 1909-1912, but we expect much more, namely every sufficiently large integer is a sum of 4 cubes.
In the frame of this understandable question, we shall illustrate how mathematicians prove weaker statements, lead computation, build models to comfort their belief in statements they cannot prove.
About the speaker
Professor Jean-Marc Deshouillers, a number theorist who has authored more than hundred research papers and advised seventeen PhD students and is currently Professor at Institut mathématique de Bordeaux, Bordeaux, France. Jean-Marc Deshouillers received his PhD in 1972 at the University Paris VI
In 1985 he showed with Ramachandran Balasubramanian and Francois Dress that, in the case of the fourth powers of Waring’s problem, the least number of fourth powers that is necessary to express any positive integer as a sum of fourth powers is 19.
Title: Zero free regions of spectral averages
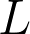
-functions
Speaker: Sandeep E. M.
Affiliation: Indian Statistical Institute, North East center.
Date and Time: September 12, 2022 at 03:30 PM
Venue: Seminar Hall, Kerala School of Mathematics
Abstract: In this talk, I would describe a recent result on the zero-free region of a weighted average of
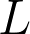
-functions of integral weight Hecke eigenforms and if time permits, some remarks on the same for those corresponding to weight zero Hecke-Maass cusp forms (level
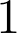
). The first is a joint work with Satadal Ganguly.
Title: Families of quadratic fields with

-rank at least

.
Speaker: Azizul Hoque
Affiliation: Rangapara College
Date and Time: August 2, 2022 at 03:30 PM
Venue: Seminar Hall, Kerala School of Mathematics
Abstract: Constructing number fields with large
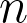
-rank has proved to be a challenging practical problem, due in part to the fact that we believe such examples to be very rare. There is a conjecture (folklore) that the
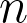
-rank of
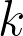
is unbounded when
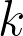
runs through the quadratic fields. It was Quer who constructed

imaginary quadratic fields with

-rank equal to
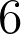
, and this result still stands as the current record. We will discuss two methods for constructing quadratic fields with large
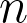
-rank. We will show that for every large positive real number
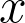
, there exists a sufficiently large positive constant

such that the number of quadratic fields with

-rank at least

and absolute discriminant
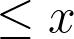
is
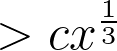
. If time permits, we will construct a parametric family of real (resp. imaginary) quadratic fields with
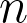
-rank at least
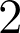
.
Title: On a Conjecture of Iizuka
Speaker: Azizul Hoque
Affiliation: Rangapara College
Date and Time: August 1, 2022 at 03:30 PM
Venue: Seminar Hall, Kerala School of Mathematics
Abstract: For any odd prime number
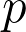
, we will construct an infinite family of quadruples of imaginary quadratic fields of the form
)
,
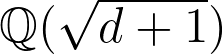)
,
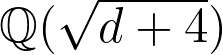)
and
)
whose class numbers are all divisible by a given odd integer

. This provides a proof of a particular case of Iizuka’s conjecture (in fact a generalization of it).
Title: Snippets from the history of Science in Ancient India.
Speaker: T. R. Govindarajan
Affiliation: The Institute of Mathematical Sciences
Date and Time: July 14, 2022 at 03:30 PM
Venue: Seminar Hall, Kerala School of Mathematics
Abstract: There are several achievements and there are failures too. Will sketch a few of these in Astronomy, Mathematics and Architecture. Will present some unsolved questions in our understanding too. Will end up with some discussions on what we gave the outside world and what we learnt.
Title : Physics and Maths of Braids and Knots:
Speaker: T. R. Govindarajan
Affiliation: The Institute of Mathematical Sciences
Date and Time: July 13, 2022 at 03:30 PM
Venue: Seminar Hall, Kerala School of Mathematics
Abstract: Braids and Knots have fascinated both Physicists and mathematicians for more than a century. I will present several developments in both the areas as well as new biological questions and end with unanswered questions.
Title : 
-units in Recurrence Sequences
Speaker: Sudhansu Sekhar Rout
Affiliation: Institute of Mathematics & Applications, Bhubaneswar
Date and Time: June 30, 2022 at 03:30 PM
Venue: Seminar Hall, Kerala School of Mathematics
Abstract: In this talk, we give various finiteness results concerning terms of recurrence sequences
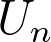
representable as a sum of

-units with a fixed number of terms. We prove that under certain (necessary) conditions, the number of indices n for which
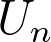
allows such a representation is finite, and can be bounded in terms of the parameters involved. In this generality, our result is ineffective, i.e. we cannot bound the size of the exceptional indices. We also give an effective result, under some stronger assumptions.
Title : Some geometric structures on principal Lie 2-group bundles over Lie groupoids.
Speaker: Praphulla Koushik
Affiliation: IISER Pune
Date and Time: June 24, 2022 at 03:30 PM
Venue: Seminar Hall, Kerala School of Mathematics
Abstract : In this talk we introduce the notion of principal Lie 2-group bundle over a Lie groupoid; as a generalisation of the notion of classical principal (Lie group) bundle over a smooth manifold. Motivated by the idea of Atiyah sequence for G-bundles over manifolds, we introduce the notion of Atiyah sequence for Lie 2-group bundle over Lie groupoids. We then see some notion of (strict) connection and semi-strict connections on such principal bundles. This is a joint work with Saikat Chatterjee and Adittya Chaudhuri
Title: On Partial Differential Equations and Diffusion Processes.
Speaker: Rajeeva Karandikar
Affiliation: Chennai Mathematical Institute.
Date and Time: May 26, 2022 at 11:00 AM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: In this talk we will describe connections between second order partial differential equations and the associated Markov processes. This connection has been an active area of research for several decades.
Title: Iwasawa theory and Galois groups
Speaker: Sujatha Ramdorai
Affiliation: University of British Columbia.
Date and Time: May 26, 2022 at 03:30 PM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: Understanding the Galois group of the field of rational numbers and of its finite extensions is one of the central problems in Number Theory. Over the last five centuries, this has led to the development of several areas within Pure Mathematics. In this talk, we shall discuss how Iwasawa theory has contributed to studying this problem.
Title: Black holes through different windows
Speaker: Ajith Parameswaran
Affiliation: International Centre for Theoretical Sciences, Tata Institute of Fundamental Research, Bangalore
Date and Time: May 25, 2022 at 03:30 PM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: Made entirely of curved spacetime, black holes are among the most enigmatic objects in the Universe. Although early theoretical ideas on objects like black holes go back to the eighteenth century, the first rigorous mathematical formulation of a black hole was made by Karl Schwarzschild in 1915, based on Einstein’s General Theory of Relativity. A variety of astronomical observations made in the last century confirmed that black holes are not just theoretical constructs — the Universe is littered with them. Recently, a variety of astronomical observations have started to probe the detailed nature of black holes. This talk will provide a summary of this exciting journey.
Title: Factorization of Integers using Rational Sieve
Speaker:Manika Gupta
Affiliation: Kerala School of Mathematics
Date and Time: April 20, 2022, 11.00 AM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: We present a discussion on different algorithms for the factorization of integers, focussing on the rational sieve. The rational sieve uses sieve theoretic methods to find the prime factors of a number. It is a special case of the General Number Field Sieve (GNFS) which is the most efficient classical algorithm for factoring ‘large’ integers. We also present a brief overview of the quadratic sieve and GNFS.
Title: A lower bound on number of representation of even numbers as sum of an odd prime and product of at most two primes
Speaker: Om Prakash
Affiliation: Kerala School of Mathematics
Date and Time: April 19, 2022, 03.00 PM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: This talk is about proving a lower bound on the number of representation of large enough even numbers as sum of an odd prime and a product of at most two primes.
Title: TBA
Speaker:Pole Vennela
Affiliation: Kerala School of Mathematics
Date and Time: April 19, 2022, 11.00 AM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: TBA
Title: Erdös Distance Problem
Speaker:Viswanathan S
Affiliation: Kerala School of Mathematics
Date and Time:April 18, 2022, 04.00 PM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: In this talk we shall introduce Erdös Distance Conjecture. This is now a glowing hot topic in mathematics. Starting with the basic sketch of the problem we shall explore certain partial bounds for the conjecture culminating in Moser’s construction. This problem has now invited tools from several fields of mathematics, some include – Fourier analysis, graph theory, and even information theory
Title: Bounded Gaps between Primes
Speaker : Viswanathan S
Affiliation: Kerala School of Mathematics
Date and Time: April 18, 2022, 11.00 AM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: In this talk we shall sketch the idea of Goldston, Pintz, and Yildirim that paved a way to attack the twin prime conjecture by establishing a connecting between equidistribution of primes in certain congruence classes and the gaps between primes (via sieve methods). Their idea later inspired Yitang Zhang and a chain of other mathematicians including Terrence Tao and James Maynard to reduce the infinitely occurring gap between successive primes which led to major breakthroughs in that field.
Title: Integers free of large prime factors
Speaker: Pole Vennela
Affiliation: Kerala School of Mathematics
Date and Time:April 17, 2022, 04.15 PM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: In this talk we are going to discuss about the number \psi(x,y) of integers < x and free of prime factors > y has been given satisfactory estimates in the regions y < (log X)3/4-6
and y > exp{(log log X)^5/3+6}. In the intermediate range, only very crude estimates have been obtained so far. We close this “gap” and give an expression
which approximates \psi(x, y) uniformly for x > y > 2 within a factor 1 + O((log y)/(log x) + (log y)/y). As an application, we derive a simple formula for \psi(cx, y)/\psi(x, y), where 1 < c < y. We also prove a short interval estimate for \psi(x, y).
Title: The Paley-Weiner Theorem
Speaker: Manika Gupta
Affiliation: Kerala School of Mathematics
Date and Time: April 17, 2022, 02.30 PM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: In this talk, a proof of the Paley-Weiner theorem is presented. The theorem relates decay properties of a function at infinity with analyticity of its Fourier transform. The theorem plays a crucial role in the proof of the main large sieve inequality. We shall also discuss the background and other applications of this result.
Title: A lower bound on number of representation of even numbers as sum of an odd prime and product of at most two primes.
Speaker:Om Prakash
Affiliation: Kerala School of Mathematics
Date and Time: April 16, 2022, 11.00 AM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: This talk is about proving a lower bound on the number of representation of large enough even numbers as sum of an odd prime and a product of at most two primes.
Title: Orthogonality of invariant vectors
Speaker: U. K. Anandavardhanan
Affiliation:Indian Institute of Technology Bombay
Date and Time: March 21, 2022 at 03:30 PM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: This talk is about finite groups and their representation theory. Given a group 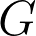 and two Gelfand subgroups
and two Gelfand subgroups 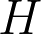 and
and 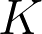 of
of 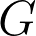 , associated to an irreducible representation
, associated to an irreducible representation 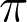 of
of 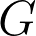 , there is a notion of
, there is a notion of 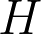 and
and 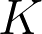 being correlated with respect to
being correlated with respect to 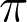 in
in 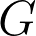 . This notion was defined by Benedict Gross in 1991. The talk will not assume much background material. Towards the end of the talk, we’ll present some recent results regarding this theme (which are joint with Arindam Jana).
. This notion was defined by Benedict Gross in 1991. The talk will not assume much background material. Towards the end of the talk, we’ll present some recent results regarding this theme (which are joint with Arindam Jana).
Title: Nice ideals, their role in ideal convergence and some thoughts
Speaker: Pratulananda Das
Affiliation: Jadavpur University
Date and Time: March 04, 2022 at 03:30 PM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: In this talk we will primarily talk about the so called “nice ideals” in the realm of set theory. We will in particular describe the very basic notion of ideal convergence to see how these ideals have been found to be very useful in summability theory before moving to more deeper observations
Title: Nice ideals, their role in ideal convergence and some thoughts
Speaker: Pratulananda Das
Affiliation: Jadavpur University
Date and Time: March 03, 2022 at 03:30 PM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: In this talk we will primarily talk about the so called “nice ideals” in the realm of set theory. We will in particular describe the very basic notion of ideal convergence to see how these ideals have been found to be very useful in summability theory before moving to more deeper observations
Title:On a family of elliptic curves of rank at least
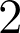
.
Speaker: Richa Sharma
Affiliation: PDF, Kerala School of Mathematics
Date and Time: 04 February 2022 at 3.30 PM
Venue: Seminar Hall, KSoM
Abstract: Let
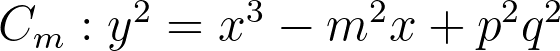
be a family of elliptic curves over
, where
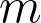
is a positive integer and
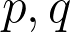
are distinct odd primes. We prove that the torsion subgroup of
)
is trivial and the
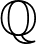
-rank of this family is at least
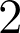
, whenever
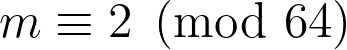
with neither
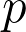
nor
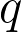
divides
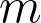
.
Title: Set partitions, tableaux, and subspace profiles under regular split semisimple matrices
Speaker: Amritanshu Prasad
Affiliation: The Institute of Mathematical Sciences
Date and Time: December 10, 2021 at 03:30 PM
Venue: Seminar Hall, Kerala School of Mathematics
Abstract: We introduce a family of univariate polynomials indexed by integer partitions. At prime powers, they count the number of subspaces in a finite vector space that transform under a regular diagonal matrix in a specified manner. At
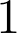
, they count set partitions with specified block sizes. At
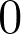
, they count standard tableaux of specified shape. At

they count standard shifted tableaux of a specified shape. These polynomials are generated by a new statistic on set partitions (called the interlacing number) as well as a polynomial statistic on standard tableaux. They allow us to express
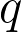
-Stirling numbers of the second kind as sums over standard tableaux and as sums over set partitions. In a special case, these polynomials coincide with those defined by Touchard in his study of crossings of chord diagrams.
Title:Lie algebras associated to closed curves on surfaces.
Speaker: Arpan Kabiraj
Affiliation: IIT Palakkad
Date and Time: November 26, 2021 at 03:30PM
Venue: Seminar Hall, Kerala School of Mathematics
Abstract:We will discuss various Lie algebras associated to closed curves on orientable surfaces (possibly with boundary and punctures) introduced by Goldman and Wolpert in the 80’s. If time permits, we will discuss a relation between these Lie algebras and skein algebras of three-manifolds.
Speaker: Aman Singh
Affiliation: Kerala School of Mathematics
Date and Time: November 19, 2021 at 03:30 PM
Venue: Seminar Hall, Kerala School of Mathematics
Title: Dirichlet’s Prime Distribution Theorem – II
Abstract: We shall see a complete proof of the fact that there are infinitely many primes in any given arithmetic progression
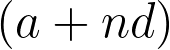)
, where
%09=%091)
.
Speaker: Aman Singh
Affiliation: Kerala School of Mathematics
Date and Time: November 17, 2021 at 04:00 PM
Venue: Seminar Hall, Kerala School of Mathematics
Title: Dirichlet’s Prime Distribution Theorem – I
Abstract: We will introduce the group of characters associated with a given finite abelian group and prove some orthogonality relations. We shall then see the Dirichlet characters and some of its properties leading up to the proof of non-vanishing of
)
for a non-principal character
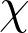
.
Title: Introduction to Hilbert modular forms and its determination by square-free Fourier coefficients.
Speaker: Rishabh Agnihotri
Affiliation: HRI, Prayagraj (Allahabad)
Date and Time: September 10, 2021 at 03:30PM
Venue: Seminar Hall, Kerala School of Mathematics
Abstract: We introduce two notions of Hilbert modular forms namely classical and adelic. After that we see the relation between them. We also talk about the determination of adelic hilbert modular forms. More concretely we discuss the following result.
Let

be as above with
)
denote its Fourier coefficients. Then there exists a square-free ideal
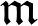
with
%5Cll%09k%5F0%5E%7B3n%2B%5Cepsilon%7DN(%5Cmathfrak%7Bn%7D)%5E%7B%5Cfrac%7B6n%5E2%2B1%7D%7B2%7D%2B%5Cepsilon%7D)
such that
%5Cneq%090)
. The implied constant depends only on
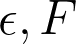
.
Title: Class group of real cyclotomic fields.
Speaker: Mohit Mishra
Affiliation: HRI, Prayagraj (Allahabad)
Date and Time: July 21, 2021 at 03:30PM
Venue: Seminar Hall, Kerala School of Mathematics
Abstract: For every finite extension of rational numbers, there is a group associated to it called the “Class Group”. Class group is a very mysterious object and there is no (infinite) family known with a prescribed class group. In 1979, G. Cornell proved that every finite abelian group 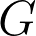 can be realized as a subgroup of a class group of infinitely many cyclotomic (totally imaginary) fields. In this talk, we will prove the analogue of this result for real cyclotomic fields. This is a joint work with L.C. Washington and R. Schoof.
can be realized as a subgroup of a class group of infinitely many cyclotomic (totally imaginary) fields. In this talk, we will prove the analogue of this result for real cyclotomic fields. This is a joint work with L.C. Washington and R. Schoof.
Title: Obstruction Theory in Algebra and Topology.
Speaker : Bibekananda Mishra
Date and time: 10.00 am to 10.45 am, 17 th June 2021.
Online platform: Zoom
Abstract: Let P be a projective module of finite rank on a ring A. What is the precise obstruction for P to have a free component (i.e. P \cong Q \oplus A)? This question, very much of algebraic flavour, is intricately related to the question of whether the vector bundles over smooth manifolds have non-vanishing sections on them. We will see in this talk certain invariants, called Nori homotopy groups, both in the algebraic as well as topological context, which gives us an effective description of the obstructions involved.
Title: A degeneration of the Compactified Jacobian of irreducible nodal curves.
Speaker: Subham Sarkar
Date and time: 12.00 pm to 12.45 pm, 17 th June 2021
Online platform: Zoom
Abstract: For each k ≥ 1, We construct an algebraic degeneration of the compactified Jacobian of a nodal curve X_k with k-nodes, over a suitable dense subset of the k-fold product of the normalisation X_0 of X_K.
A special fiber is isomorphic to the Jacobian of X_0 and k-fold product of a rational nodal curve.
We prove that the total space is a quasi-projective variety with k-th product of normal crossing singularity.
As an application we computed the mised Hodge number of the cohomogy of compactified Jacobian.
Title: Shifted convolution sums and sign changes of Fourier coefficients of certain automorphic forms.
Speaker: Lalit Vaishya
Date and time: 3.00 pm to 3.45 pm, 17 th June 2021
Online platform: Zoom
Abstract: Briefly, we present some of our work which deal with some problems in the theory of automorphic forms. In the first part, we discuss some problems on shifted convolution sums associated to Hecke Maass cusp forms (non holomorphic cusp forms), holomorphic Hecke eigen (cusp) forms and obtain the estimates. In the second part, we prove a quantitative result about sign changes of Fourier coefficients of Hecke eigenform supported at positive integers represented by a primitive integral positive binary quadratic from of negative discriminant having class number 1. We also study the average behavior of Fourier coefficients of Hecke eigenforms supported at positive integers represented by a primitive integral positive definite binary quadratic form of negative discriminant having class number 1. As a consequence, we prove that there are infinitely many sign change of sequence of Fourier coefficients supported at positive integers represented by these binary quadratic forms.
Title: On the Topology of Complex Projective Varieties
Speaker: NimaRose Manjila
Affiliation: IISER Pune
Date and Time: April 09, 2021 at 02:00PM
Venue: Seminar Hall, Kerala School of Mathematics
Abstract: We use Morse Theory and Lefschetz Pencil to find the Topology of Complex Projective Curves and generalise this idea to prove Lefschetz Theorem. Other results include a proof of Poincare Duality and Riemann Hurwitz theorem for Ramified Covers of Curves.
Title: Real Unipotent Elements in Classical Lie Groups.
Speaker: Krishnendu Gongopadhyay
Affiliation: IISER Mohali
Date and Time: April 08, 2021 at 03:30PM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: Real elements are those elements in a group which are conjugate to their own inverses. Real elements appear naturally at different branches of mathematics. These elements are also known as `reversible’ elements in the literature. These elements are closely related to the so-called strongly real elements in a group which are products of two involutions. After giving a brief exposition on real elements in groups, I shall discuss classification of real unipotent elements in classical Lie groups which is part of a joint work with Chandan Maity.
Title: A generalized modified Bessel function and explicit transformations of certain Lambert series
Speaker:Rahul kumar
Date and Time: March 26, 2021 at 04:00PM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: An exact transformation, which we call a master identity, is obtained for the series P∞n=1 σa(n)e−ny for a ∈ C and Re(y) > 0. As corollaries when a is an odd integer, we derive the well-known transformations of the Eisenstein series on SL2 (Z), that of the Dedekind eta function as well as Ramanujan’s famous formula for ζ(2m + 1). Corresponding new transformations when a is a non-zero even integer are also obtained as special cases of the master identity. These include a novel companion to Ramanujan’s formula for ζ(2m+ 1).Although not modular, it is surprising that such explicit transformations exist. The Wigert-Bellman identity arising from the a = 0 case of the master identity is derived too. The latter identity itself is derived using Guinand’s version of the Vorono ̈ı summation formula and an integral evaluation of N. S. Koshliakov involving a generalization of the modified Bessel function Kν(z). Koshliakov’s integral evaluation is proved for the first time. It is then generalized using a well-known kernel of Watson to obtain an interesting two-variable generalization of the modified Bessel function. This generalization allows us to obtain a new transformation involving the sums-of-squares function rk(n). This is joint work with Atul Dixit and Aashita Kesarwani.
Title: Weak Mordell-Weil Theorem for Chow groups over global function fields
Speaker:Kalyan Banerjee
Date and Time: March 26, 2021 at 03:00PM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: The classical weak Mordell-Weil theorem for an abelian variety A over a number field K says that A(K)/nA(K) is finite for any integer n bigger than 1. This has further consequence that the group A(K) of K-rational points on A is finitely generated. In this talk we are going to consider a variety X defined over the algebraic closure of a function field of a smooth projective curve and consider the group of degree zero cycles modulo rational equivalence on this variety denoted by A_0(X). We are going to consider the question analogous to the weak Mordell-Weil theorem for the Galois invariants of A_0(X), that is whether the group A_0(X)^G/nA_0(X)^G is finite, where G is the absolute Galois group of the function field and n is an integer bigger than 1. We are going to prove this analogue under some assumption on the variety X.
Title: Representation theory of finite groups – an Introduction – II.
Speaker: Hassain M
Affiliation: Kerala School of Mathematics
Date and Time: March 17, 2021 at 02:00PM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: Let
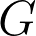
be a finite group. A
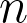
-dimensional representation of
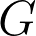
is a homomorphism from
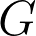
to the group
)
of
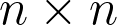
invertible matrices over

In this talk, I will discuss some interesting examples and basic results in representation theory of finite groups.
Title: Arakelov Geometry of Modular Curves
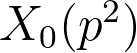)
.
Speaker: Chitrabhanu Chaudhuri, NISER Bhubaneshwar
Date and Time: March 12, 2021 at 03:30PM
Venue: Seminar Hall, Kerala School of Mathematics (online lecture)
Abstract: I shall outline the construction of a semisimple and minimal regular model for
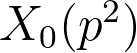)
over an appropriate number field. This will be a regular scheme over the spectrum of the ring of integers of that number field, such that the fibres are complete curves with at worst nodal singularities and satisfying certain stability conditions. The generic fibre of the model is isomorphic to
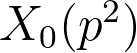)
. The purpose of this construction is to use the theory developed by Shou-Wu Zhang, using Arakelov theory, for proving an effective version of a conjecture by Bogomolov in this special case of modular curves
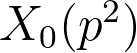)
.
Title: Representation theory of finite groups – an Introduction – I.
Speaker: Hassain M
Affiliation: Kerala School of Mathematics
Date and Time: March 10, 2021 at 02:00PM
Venue: Seminar Hall, Kerala School of Mathematics.
Abstract: Let
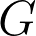
be a finite group. A
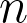
-dimensional representation of
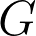
is a homomorphism from
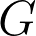
to the group
)
of
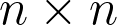
invertible matrices over

In this talk, I will discuss some interesting examples and basic results in representation theory of finite groups.
Title: Noncommutative Korovkin Theory.
Speaker: Arunkumar C. S.
Affiliation: Kerala School of Mathematics
Date and Time: February 26, 2021 at 03:00PM
Venue: Seminar Hall, Kerala School of Mathematics
Abstract: In this talk, we will introduce the Hyper Rigidity of operator systems in  -algebras as a non commutative analogue of Korovkin sets in the space of continuous functions,
-algebras as a non commutative analogue of Korovkin sets in the space of continuous functions, ![C[0,1] C[0,1]](https://ci4.googleusercontent.com/proxy/VnoiY1PstEHeDXWmWQ4DBi29l5pcnqpXyUzyax-_IBG5YhJ6YlWLn8lwo4EvJcqZ_msM9c_Jb8MVLjUv_IZa9R1ayFl8HDIOnEzOdMdaAOYqFEyVuB4CSyxD=s0-d-e1-ft#https://s0.wp.com/latex.php?zoom=3&bg=ffffff&fg=000000&s=0&latex=C[0,1]) . Also, we point out one of our recent results, and a couple of open questions along this direction.
. Also, we point out one of our recent results, and a couple of open questions along this direction.
Title: A certain kernel function for -values of half-integral weight Hecke eigenforms.
Speaker: Sreejith M. M.
Affiliation: Kerala School of Mathematics
Date and Time : February 05, 2021 at 03:00 p.m.
Venue : Seminar Hall, Kerala School of Mathematics
Abstract: In this talk we will derive a non-cusp form of weight

(

, even) for
)
in the Kohnen plus space whose Petersson scalar product with a cuspidal Hecke eigenform
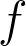
is equal to a constant times the
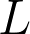
value
.)
We also prove that for such a form
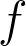
and the associated form
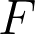
under the
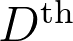
Shimura-Kohnen lift the quantity
L(F,2k-1)%7D%7B%5Cpi%5E%7Bk-1%7D%5Clangle%09f,f%5Crangle%09L(D,k)%7D)
is algebraic.
Title: Characterization of linear maps preserving unitary conjugation.
Speaker: Dr. Shankar P.
Affiliation: Indian Statistical Institute, Bangalore
Date and Time: January 22, 2021 at 03:00PM
Venue: Seminar Hall, Kerala School of Mathematics
Title: Sign Changes in restricted coefficients of Hilbert Modular forms
Speaker: Krishnarjun K
Affiliation: Harish Chandra Research Institute, Prayagraj(Allahabad)
Date and Time: January 08, 2021 at 03:00PM
Venue: Seminar Hall, Kerala School of Mathematics
Abstract: Let

be an adelic Hilbert cusp form of weight
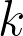
and level

over a totally real number field
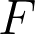
. In this talk, we study the sign changes in the Fourier coefficients of

when restricted to square-free integral ideals and integral ideals in an “arithmetic progression”. In both cases we obtain qualitative results and in the former case we obtain quantitative results as well. Our results are general in the sense that we do not impose any restriction of the number field
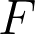
, the weight
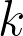
or the level

.
Title : Some notions of non-commutative convexity
Speaker: Syamkrishnan M. S.
Affiliation: Kerala School of Mathematics
Date and Time: December 04, 2020 at 03:00PM
Venue: Seminar Hall, Kerala School of Mathematics
Abstract: In this talk, we shall introduce two non-commutative versions of the classical convexity, namely the

-convexity and matricial convexity in the setting of

-algebras. We shall discuss the similarities as well as dissimilarities between the convex sets in the classical setting with the convex sets in the non commutative case. Also, we will be discussing its connections with other areas of operator algebras.
Title: On non-vanishing of modular L functions inside the critical strip
Speaker : Sandeep E. M.
Affiliation : Kerala School of Mathematics
Date and Time : November 20, 2020 at 03:00 p.m.
Venue : Seminar Hall, Kerala School of Mathematics
Title : Elliptic Curves: Introduction and An Application
Speaker: Kalyan Chakraborty
Affiliation: Kerala School of Mathematics
Date and Time: November 06, 2020 at 03:00 p.m.
Venue: Seminar Hall, Kerala School of Mathematics
Abstract: This talk will begin with an introduction to elliptic curves. We shall then progress into the BSD conjecture and finally look into the idea of the proof of Fermat’s last theorem.
Title: An invitation to the theory of L functions
Speaker : Krishnarjun K
Affiliation : Harish Chandra Research Institute, Prayagraj(Allahabad)
Date and Time : October 23, 2020 at 03:00 p.m.
Venue : Seminar Hall, Kerala School of Mathematics
Abstract : The aim of this talk is to introduce the notion of an 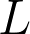 function and to describe a few basic properties. We shall also prove two classical theorems, one of Riemann and Dirichlet and demonstrate how techniques from complex analysis can be used to prove arithmetic results. We shall briefly touch upon current research topics of interest in the subject, if time permits.
function and to describe a few basic properties. We shall also prove two classical theorems, one of Riemann and Dirichlet and demonstrate how techniques from complex analysis can be used to prove arithmetic results. We shall briefly touch upon current research topics of interest in the subject, if time permits.
Here is a list of the previous colloquiums and seminars
-power property in rings
-function around elliptic points.
and two Gelfand subgroups
and
of
, associated to an irreducible representation
of
, there is a notion of
and
being correlated with respect to
in
. This notion was defined by Benedict Gross in 1991. The talk will not assume much background material. Towards the end of the talk, we’ll present some recent results regarding this theme (which are joint with Arindam Jana).
can be realized as a subgroup of a class group of infinitely many cyclotomic (totally imaginary) fields. In this talk, we will prove the analogue of this result for real cyclotomic fields. This is a joint work with L.C. Washington and R. Schoof.
-algebras as a non commutative analogue of Korovkin sets in the space of continuous functions,
. Also, we point out one of our recent results, and a couple of open questions along this direction.
be a complex separable Hilbert space and let
be the algebra of all bounded linear operators on
. In this talk, we discuss about what are the linear maps
which satisfy
on
.
-series associated to a classical modular form
(of weight
and level
) denoted by
denotes the
Fourier coefficient of
(in its
-series expansion around
) is an analytic function on the right half plane
and can be analytically continued to the whole
. The non-trivial zeros of this function lie inside the critical strip
. The analogue (GRH) of the Riemann Hypothesis in this context states that they all lie on the critical line
itself.
is an absolute constant, is currently known to be a zero-free region for
. Some aspects of this non-vanishing related to my work will be discussed in this talk. This is a joint work with Prof M Manickam and Prof V Kumar Murty
function and to describe a few basic properties. We shall also prove two classical theorems, one of Riemann and Dirichlet and demonstrate how techniques from complex analysis can be used to prove arithmetic results. We shall briefly touch upon current research topics of interest in the subject, if time permits.









